Source: School of Computer Science and Engineering
Edited by: Zheng Longfei, Wang Dongmei
Recently, the team of Associate Researcher Xie Jiarong from the School of Computer Science and Engineering at Sun Yat-sen University published a research article entitled "Indirect influence in social networks as an induced percolation phenomenon" in the Proceedings of the National Academy of Sciences (PNAS). Through the statistical analysis of empirical data on collaboration behaviors of scientists, it is found that indirect collaborators can dominate over direct collaborators in shaping scientists’ behaviors. And based on this empirical phenomenon, an induced percolation model for behavioral propagation is proposed, which provides a research framework for behavioral communication with indirect effects.
Percolation is one of the important research directions of statistical physics. Over the past 20 years, scientists have continuously used percolation models to study propagation problems in complex networked systems. To the best of our knowledge, almost all percolation theories focus on modeling influence mechanisms between direct neighbors. However, growing evidence in social and ecological systems suggests that indirect influence is pervasive in dynamical behaviors of the system.
For example, the Three Degrees of Influence Rule in social networks shows that in social behaviors such as drug abuse, alcoholism, obesity, divorce, among others, you can be significantly influenced by friends of friends of friends. Despite the ubiquity of indirect influence in real-world systems, few studies have examined the exact mechanisms by which indirect influence occurs.
Using large-scale data on collaboration behaviors among scientists, this work provides a detailed study of the dynamical process by which scientists change their research fields and finds that indirect collaborators dominate over direct collaborators in impacting the changes. This phenomenon exists in many hot fields, such as complex networks, graphene, quantum science.
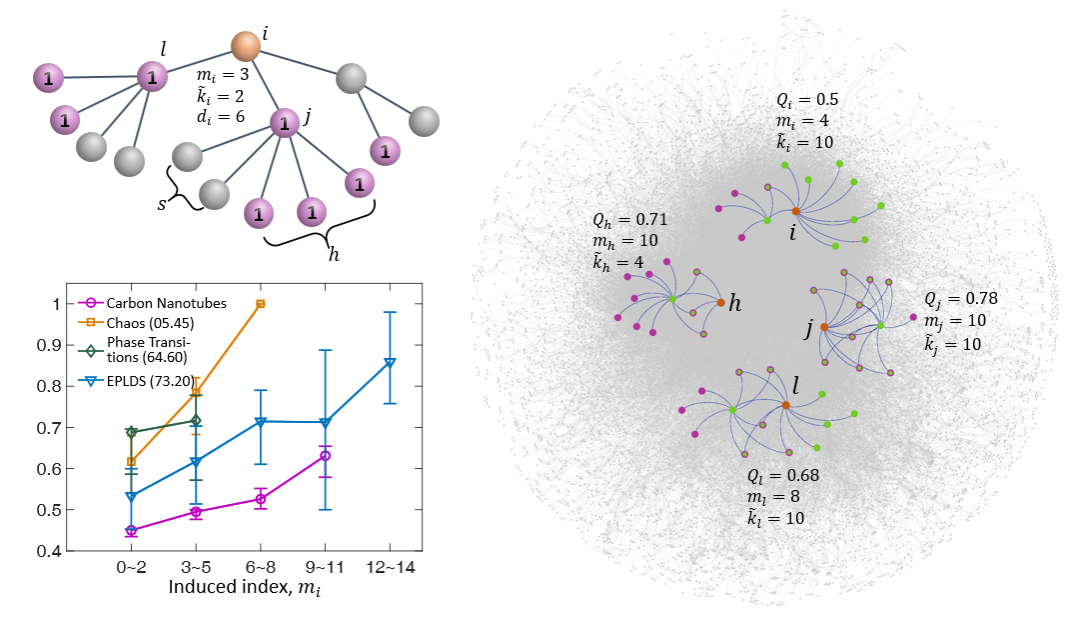
Figure 1: Empirical analysis shows the existence of indirect influence mechanisms in collaboration networks of scientists.
Inspired by the above empirical phenomenon, the research team proposed an induced percolation model. Through analytical and numerical analysis, it is founded that the indirect influence mechanism drives the system to produce a plethora of rich phase transition behaviors: for example, the directionality of network edges can change the type of percolation phase transition: in directed, undirected and mixed networks, it shows first-order, second-order and hybrid phase transitions; near the critical point of the second-order phase transition, the connectivity of the network exhibits a novel oscillatory-like behavior. These differ markedly from nearly all known connectivity behaviors on complex networks. This means that the proposed induced percolation may profoundly reveal important yet hidden relationships between the asymmetrical indirect interactions and the macroscopic phase transition behavior of the system.
This result is another significant progress made by Associate Researcher Xie Jiarong and his collaborators following the previous results, the cover story about information diffusion and percolation phase transitions on social media published in Nature Human Behavior in 2021. The research is supported by the National Natural Science Foundation of China (No. 61903385) and others.
Link to the article: https://www.pnas.org/content/119/9/e2100151119
